This is Part II of a quantum computing collaboration series with Professor Isaac Kim, Assistant Professor of Computer Science at UC Davis. [Part I here]
(1) Difficulty Level: High School
(1.1) What makes a quantum computer different from the laptop I’m using now?
(1.2) Is quantum computing just science fiction, or is it actually real today?
(1.3) Why do people say quantum computers are “in two places at once”?
(1.4) Can a quantum computer break my Bitcoin wallet?
(1.5) What does it mean to make crypto “quantum-safe”?
(2) Difficulty Level: College
(2.1) Why is making crypto quantum-resistant so hard if we already have post-quantum algorithms?
(2.2) Why is quantum error correction so central, and how do we know it actually works?
(2.3) How will we know when quantum computers are getting dangerous for crypto?
(2.4) What exactly is a ‘logical qubit’ and why do we need thousands of physical ones to make just one?
(2.5) Are all blockchains equally vulnerable to quantum attacks or are some safer?
(3) Difficulty Level: Pro
(3.1) How can Shor’s algorithm break ECC?
(3.2) Why are PQC schemes secure against quantum attacks?
(3.3) I heard that there are new improved quantum algorithms for breaking ECC. Should I be concerned?
(3.4) Is it true that there are new quantum error correcting codes that are more efficient, and what is their relevance to crypto?
(3.5) If somebody builds a large-scale quantum computer for breaking crypto, how fast can it break ECC?
Foreword
When we published Quantum Computing x Crypto: Everything You Need to Know, our goal was to demystify a topic that most crypto people (myself included, initially) felt was either too abstract or too far away to matter. There’s a lot of hype and noise around quantum computing, and most explanations relevant to crypto (even well-intentioned ones) are either too hand-wavy or too academic. So we teamed up with someone who could actually speak with authority.
Isaac Kim is a quantum computing researcher and Assistant Professor of Computer Science at UC Davis. He did his undergrad at MIT, his PhD at Caltech, and has held research positions at IBM, Stanford, and the Perimeter Institute. He’s also worked in industry as a quantum architect at PsiQuantum and taught at the University of Sydney. His work focuses on making quantum computers actually usable: improving reliability, managing error correction, and designing systems that can scale. He understands both the theory and the bottlenecks, which is exactly what we wanted for a report that focused on the practical intersection between quantum computing and crypto.
It was great to see the audience enjoy Part I, and given the complexity of the topic, we received a lot of questions - this follow-up report is designed to answer those.
Some questions were simple: What is a qubit? Can quantum computers actually steal my Bitcoin? Others more technical: What’s a logical qubit? How many gates do you need to break ECC? How do we know error correction even works? And some are just the kind of questions that come up when you’ve read Part I and start thinking a little deeper.
We thought a Q&A format would be the most honest way to tackle this.
We hope this report helps bridge the gap for the crypto-native reader to understand where the industry stands in the light of the fast progressing field of quantum computing.
– Rick
Presto Research
1. Difficulty Level: High School
1.1 What makes a quantum computer different from the laptop I’m using now?
Anything that a classical computer can do, a quantum computer can do, too. However, quantum computers have additional capabilities, such as superposition and entanglement, that are not available in classical computers. For some problems, like code-breaking and simulation of physical systems, these additional capabilities become very handy, leading to an exponential speedup. However, for some problems these additional capabilities do not seem to be very useful, like in optimization.
Figure 1: Quantum Computers Differ from Classical Computers in Many Ways

Source: Presto Research
Superposition: The quantum property that allows a qubit to exist in a blend of both 0 and 1 simultaneously, enabling massive parallelism in computation not possible in classical systems. See Question 1.3 below.
Entanglement: A uniquely quantum mechanical property where two or more qubits are linked such that the state of one immediately affects the state of the other(s), regardless of distance. Entanglement is essential for quantum teleportation, superdense coding, and many quantum algorithms.
1.2 Is quantum computing just science fiction, or is it actually real today?
Quantum computing is very real. Scientists and engineers have built machines that can run small quantum programs and demonstrate key behaviours like entanglement and superposition. Companies like IBM, Google, and newer players like Quantinuum have developed working quantum computers with over 100 qubits.
But here’s the catch: we need millions of high-quality qubits to break strong encryption or run useful applications at scale. Today’s systems still make too many errors and can only handle short, simple tasks. So while quantum computing has moved beyond science fiction, it is not yet powerful enough to pose a serious threat to crypto or change everyday computing. Still, progress is steady, and while it may be a work in progress, it it no longer hypothetical.
Qubit: The fundamental unit of quantum information, which can exist in a superposition of the classical 0 and 1 states. Qubits enable parallelism and entanglement, powering the advantages of quantum computing over classical systems.
1.3 Why do people say quantum computers are “in two places at once”?
This is to describe a phenomenon called superposition. When a bit is in a superposition, it can be in a special state of being both 0 and 1 at the same time. A surprising fact is that this phenomenon can be utilized to get computational seedups, for problems like factoring large numbers or breaking encryption.
1.4 Can a quantum computer break my Bitcoin wallet?
Yes, quantum computing matters to crypto because it threatens the kind of encryption that blockchains rely on, especially elliptic curve cryptography (ECC) which secures most wallets. Quantum computers could one day run Shor’s algorithm, a powerful technique for breaking ECC and recovering private keys from public ones. That means if your wallet’s public key is exposed, a future quantum attacker could steal your funds.
However, this isn't possible today. Quantum computers aren’t yet powerful enough: they’d need thousands of high-quality qubits working almost flawlessly. But the risk is real in the long term, which is why the crypto community is already exploring quantum-resistant alternatives. Wallet design also matters: if your public key isn’t visible on-chain until you spend, you’re better protected. So while your Bitcoin is safe for now, preparing for future quantum attacks is already a priority.
Elliptic Curve Cryptography (ECC): A public-key cryptosystem that uses the algebraic structure of elliptic curves over finite fields to offer high security with small key sizes. Efficient and widely adopted, ECC is considered vulnerable to quantum attacks, particularly Shor’s algorithm, which could break it in polynomial time.
Shor's Algorithm: A quantum algorithm that factors large integers in polynomial time, breaking the security of classical cryptographic schemes like RSA (Rivest–Shamir–Adleman) and ECC, and motivating the need for post-quantum cryptography.
1.5 What does it mean to make crypto “quantum-safe”?
To make crypto quantum-safe means to protect it from future quantum attacks. Right now, most blockchains rely on encryption that’s secure against regular computers but vulnerable to quantum ones, especially when it comes to public key cryptography. “Quantum-safe” or post-quantum cryptography (PQC) uses new algorithms that can withstand attacks from both classical and quantum computers. These include lattice-based cryptography and hash-based signature schemes.
Switching to quantum-safe systems has the sole goal to make sure your assets and communications stay safe no matter what kind of computer is trying to break in, but it does mean using bigger keys and slower signatures.
Post-Quantum Cryptography (PQC): A branch of cryptography focused on developing secure algorithms resistant to quantum attacks, often based on hard lattice problems, hash functions, or code theory, to replace vulnerable schemes like RSA and ECC.
2. Difficulty Level: College
2.1 Why is making crypto quantum-resistant so hard if we already have post-quantum algorithms?
The main trouble with the PQC schemes (one-time signatures, NIST-approved public-key systems) is that they introduce overhead in key size/speed/usability. So if we were to upgrade the existing cryptographic schemes to PQC, things will be slower, expensive, and more clunky.
In particular, on-chain execution of PQC can be computationally demanding, to the extent that they will likely never be used.
While post-quantum wallet exist (like for ETH and SOL), these are still the exception rather than the norm. And again, the same issue applies. From a user perspective, it just doesn’t seem to make sense to migrate to PQC schemes when they only deteriorate the current user experience.
Overhead: The additional computational cost introduced by quantum error correction, which multiplies the number of logical operations needed to compensate for noise and maintain reliability.
2.2 Current State of Quantum Hardware
Since Shor discovered his famous algorithm for breaking RSA, a big effort in quantum computing has always been to answer this question: when can we break RSA using a quantum computer? This is a very well-studied subject, and long story short, we expect we’ll need thousands of nearly flawless qubits, executing billions and even trillions of gates. Unfortunately, in the existing quantum computers, the gates fail roughly one out of thousand times. So if you run these quantum algorithms on today’s quantum computer, they will just output essentially garbage. Quantum error correction is the only game in town that lets us build such a large scale and reliable quantum computer.
For almost twenty years, quantum error correction was just a theoretical concept, and understandably there were some skeptics. However, the good news is that finally we are entering an era of QEC. These days, there are so many experiments, both in industry and academia, that demonstrate that quantum error correction works. At the end of the day, what these experiments achieve is simple: reducing the rate at which error occurs by detecting and removing them.
Gate: This is a basic operation that changes the state of one or more qubits. Like logic gates in classical computing, quantum gates manipulate information but instead of flipping bits, they apply precise transformations to qubits using quantum mechanics, enabling phenomena like superposition and entanglement.
Error Correction: The process of detecting and correcting errors in quantum states without directly measuring the qubit. It involves encoding logical qubits using multiple physical qubits to protect against bit-flip, phase-flip, and more complex noise, essential for building fault-tolerant quantum computers.
2.3 How will we know when quantum computers are getting dangerous for crypto?
I would say the first biggest warning sign would be when we start to have a quantum computer with roughly 100 logical qubits and the logical error rate of< 10⁻⁵. This isn’t enough to break crypto, but building a machine like this is a strong indication that crypto will be broken in the imminent future. Any technology capable of building a machine like this will likely be mature enough to build an even larger machine, capable of breaking crypto.
One more thing to add is that a lot of the companies are aiming to build exactly a machine like this. Most likely, we won’t be seeing these machines anytime soon, certainly not over the next 2~3 years. However, it is conceivable that a machine like this can be built in five years, because that is exactly the plan of many quantum computing companies, like Google, PsiQuantum, QuEra, etc.
Figure 2: Quantum Computing Scaling
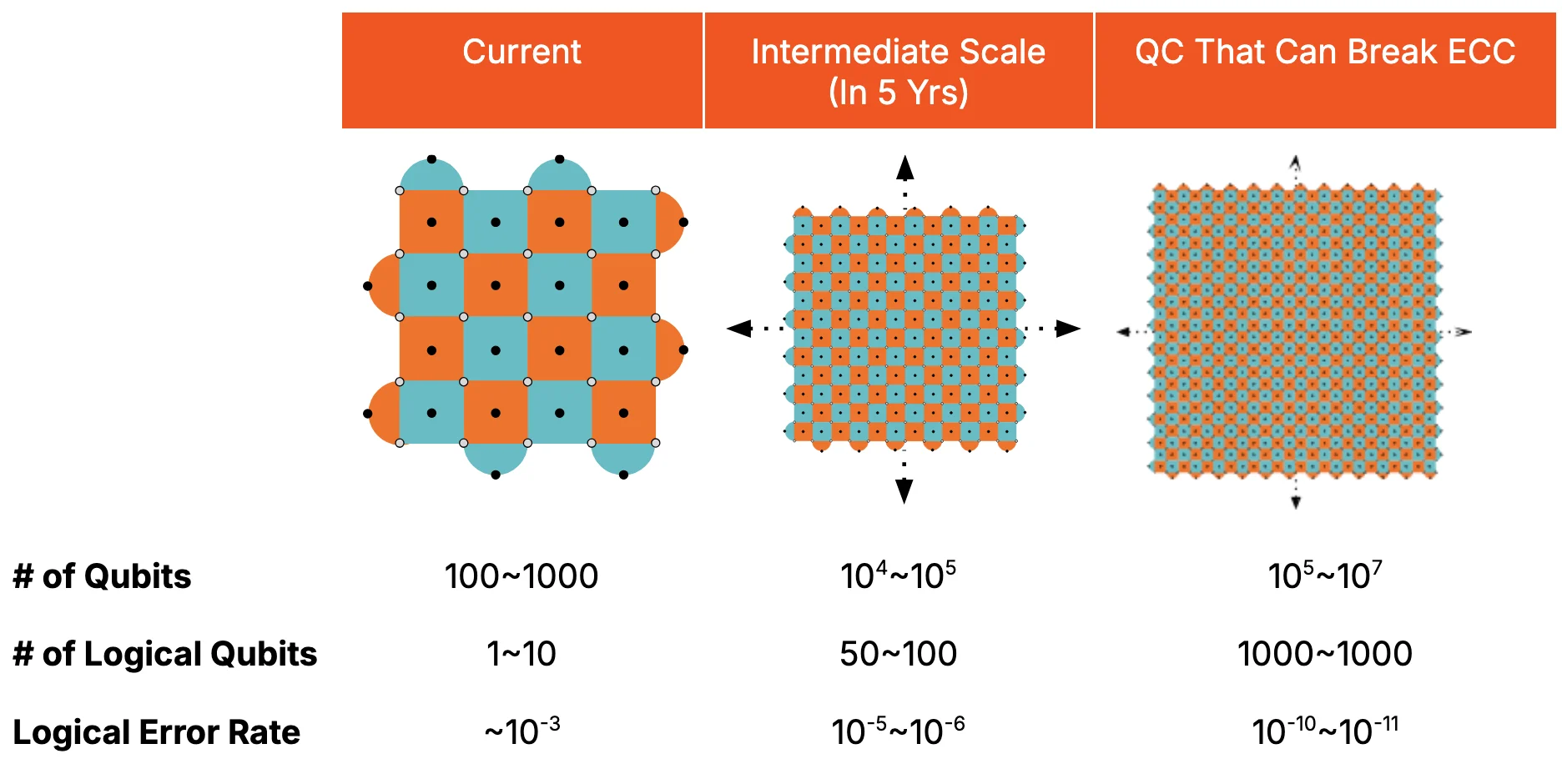
Source: Presto Research
2.4 What exactly is a ‘logical qubit’ and why do we need thousands of physical ones to make just one?
A logical qubit is really a collection of physical qubits (atoms, ions, superconducting qubits), which altogether store a single qubit worth of information. Even though this leads to a large overhead (by a factor of 50x-1000x), there is a huge benefit. The larger overhead we pay, the better logical error rate we get, because we get to correct more errors.
We should also note that the overhead is not a fixed number. We can pay a small overhead, but the price we have to pay is that the error correction capability will not be so great. On the other hand, if we pay a larger amount of overhead, we will be able to correct more errors. So really the question is how much overhead we should pay to get the logical error rate low enough to break crypto (like 10⁻⁸ to 10⁻¹¹). This number turns out to be a few hundred to a thousand. There are more recently proposed architectures which, under optimistic assumptions, can bring down this number to maybe 50. But this is an area of active research, and pretty far from being implemented in a commercial product.
Logical Qubit: A qubit that represents encoded quantum information protected by error correction across multiple physical qubits. Logical qubits behave like ideal qubits, even in the presence of noise, and are essential for fault-tolerant quantum computing.
2.5 Are all blockchains equally vulnerable to quantum attacks or are some safer?
Any blockchain that uses ECC, like Bitcoin and Ethereum, are vulnerable. There are some slight differences in the degree of vulnerability. For instance, Ethereum always reveals public keys whereas Bitcoin only does so after a transaction. Hence, unused wallets are safer. Also, PQC wallets exist for ETH and SOL, but they have not seen mainstream adoption yet. There are some chains that use quantum-resistant cryptography. However, they have not been rigorously vetted yet.
So to summarize, majority of the blockchains will be eventually vulnerable to quantum attacks. In order to protect the assets, one must implement PQC schemes and vet the security by rigorous testing.
3. Difficulty Level: Pro
3.1 How can Shor’s algorithm break ECC?
Shor’s original paper on factoring actually solves a much broader problem called period finding. Quantum computers are very good at finding a period of a given function, a capability that classical computers lack. A well-known fact about both RSA and ECC is that they can be broken if we can compute the period efficiently. Since a part of Shor’s algorithm solves this period finding problem, it can be also used to break ECC.
3.2 Why are PQC schemes secure against quantum attacks?
There are really two types of PQC schemes. One is based on a one-time signature and the other is based on lattice-based cryptography. For the former, the security of the scheme is based on quantum computer’s inability to invert cryptographic hash functions, which is a widely accepted assumption. As such, there is very little doubt that one-time signatures will be secure against quantum attacks.
For the latter, the security of the lattice-based schemes rely on our belief that quantum computers cannot solve a problem known as the shortest vector problem. While we do not expect quantum computers to be able to solve this problem efficiently, our only evidence for this is our inability to come up with an efficient quantum algorithm. In that sense, the security of the lattice-based schemes is on a less firm ground than that of one-time signature.
To summarize, the security of both schemes rely on a problem that a quantum computer likely cannot solve efficiently. However, the security of the one-time signature is on a more firm ground than that of the lattice-based schemes.
Shortest Vector Problem (SVP): This is a foundational problem in lattice-based cryptography. It asks: given a lattice (a regular grid of points in space), what is the shortest non-zero vector in that lattice? Finding this shortest vector is computationally hard, especially in high dimensions, which makes it useful for designing quantum-resistant cryptographic schemes.
3.3 I heard that there are new improved quantum algorithms for breaking ECC. Should I be concerned?
There was a recent paper by Litinski that made a big splash. It claimed that there are quantum computing architectures that can compute 256-bit ECC private key using around only 50 million gates. This is a substantially lower number than what people used to think, leading to a concern that ECC may be broken in a timeline that is much shorter than what people have imagined.
However, there are two important caveats to this paper. The first caveat is that 50 million is the number of gates used per private key, if we want to obtain a large number of private keys. The key idea is that part of the computation used for obtaining one private key can be reused to obtain another private key. So if we want to obtain many private keys, the part that is being reused needs to be done only once. The number of 50 million is obtained after removing the part that are reused repeatedly. This can speed up the rate at which the private keys are obtained once a large-scale quantum computer is available. However, it does not fundamentally change the resource needed to break ECC; that still requires building a quantum computer consisting of millions of qubits.
The second caveat is that the overall cost is quantified using a concept called active volume. This concept was advocated in a paper by Litinski and Nickerson, and the key point of the paper is that the footprint of the quantum computer can be reduced substantially by introducing some nonlocal connection between different quantum computing module. This idea can be realized using photonic interconnects, making this approach somewhat realistic. However, introducing such nonlocal connection complicates the design of the architecture. As such, we do not expect the first few generations of fault-tolerant quantum computer to be able to optimize the active volume.
To summarize, the techniques used in the new algorithm for breaking ECC does not bode well with the early generation fault-tolerant quantum computers. Therefore, we do not expect this algorithm to shorten the timeline of breaking the ECC.
Nonlocal Connectivity: The ability for qubits in a quantum computer to interact with each other even when they are not physically adjacent. In systems with nonlocal connectivity (like trapped ions or photonic qubits), any qubit can potentially interact with any other, which simplifies circuit design and reduces the number of operations needed to perform complex algorithms.
Photonic Interconnects: Channels that use light (photons) instead of electrical signals to transfer quantum information between qubits or between different modules in a quantum computer. Photonic interconnects are especially important for scaling quantum systems, as they enable fast, low-noise communication across physically separated components without introducing significant decoherence.
3.4 Is it true that there are new quantum error correcting codes that are more efficient, and what is their relevance to crypto?
As we have discussed in Part I, the biggest challenge in building a reliable quantum computer is quantum error correction. For a very long time, the leading candidate scheme was based on an error correcting code known as the “surface code.” This is a code that is the default method of choice for various reasons. It is simple, flexible, and compatible with virtually every quantum computing platform. However, a big downside of this approach has been the overhead. To build a quantum computer capable of breaking ECC using this approach, one would need roughly hundreds to a thousand physical qubits to get one good logical qubit.
That status quo might be changing, due to the advent of new error correcting codes called quantum low-density parity check (QLDPC) codes. These are codes that require a large amount of nonlocal connection between qubits, and using these codes will be likely harder. However, these codes have a great theoretical promise in that the overhead can be reduced substantially, by a factor of 10 or more. This approach is currently being vigorously studied, although mostly on a theoretical level.
There are several major hurdles that need to be overcome for this approach to work. The primary one lies in technological development. Unlike the surface code-based scheme, QLDPC codes require nonlocal connectivity. While this is available by default in some platforms (ions, photons, neutral atoms), it is more challenging in other platforms, e.g., superconducting qubits. Optimizing the nonlocal connectivity required for QLDPC codes is a major challenge, and it is far from clear how to achieve that. Another major issue is that running computation on QLDPC codes is much more complicated than running it on the surface code. The latter is extremely well-understood at the moment whereas the former is still an area of active research. While current research is showing a lot of promise, more work is needed to understand whether building a quantum computer using QLDPC code is genuinely better than building it using the surface code.
When it comes down to the implication in crypto, it seems unlikely that the QLDPC code-based quantum computer will be available in the first few generations of fault-tolerant quantum computers. This is for a simple reason that QLDPC code is a rapidly evolving field, and it seems rather risky to base the first-generation architecture on this less understood approach. For most quantum computing companies, likely the surface-code base method would be the leading approach to building their early generation quantum computers. As such, it seems unlikely that these new approaches will substantially change the timeline of building a quantum computer capable of breaking ECC.
Surface Code: A widely used quantum error correction code that arranges qubits on a 2D grid with only local interactions, valued for its simplicity and hardware compatibility but known for high qubit overhead.
Quantum LDPC (Low-Density Parity Check) Code: A newer class of error correction codes that offer lower overhead by using sparse but nonlocal qubit connections, promising major efficiency gains but requiring more complex architectures.
3.5 If somebody builds a large-scale quantum computer for breaking crypto, how fast can it break ECC?
This is a challenging question that depends on a lot of details. However, there is a somewhat simplistic method that will give a good ballpark number. At least for the first few generations of fault-tolerant quantum computers, it is very likely that quantum computers will have a limited degree of parallelism. This means that certain logical gates (such as Toffoli gate) will be likely applied serially, one by one.
For this reason, the time to run an algorithm can be calculated using the following formula:
Computation Time = Gate Time x Time Overhead x Number of logical gates
The gate time refers to the time to execute gates at the physical level. For superconducting qubits, this number can be as low as tens of nanoseconds. For ion trap quantum computers, this number is substantially slower, on the order of 100μs - 1ms. The time overhead refers to the blowup in the number of computation steps due to quantum error correction. As of now, it is expected this number to be around 20-30. As for the number of logical gates, even in an optimistic scenario, breaking ECC is expected to require 50 million gates per private key. More realistically, his number will likely go up to around 200-300 million gates.
Plugging in these numbers, we end up getting drastically different numbers for superconducting qubits and ion trap-based qubits. For the superconducting qubits, it would take anywhere between 1-15 minutes. For ion trap-based qubits, we will get anywhere between 100 hours - 2500 hours. This shows that, even if a large-scale quantum computer is built, the actual computation time to break ECC can be drastically different depending on a number of assumptions. In particular, technologies with a slower clock speed, such as ion traps, may be too slow for rapid decryption of the private keys.
Parallelism: The ability of a quantum computer to perform multiple operations at the same time. Limited parallelism means gates must be applied in sequence, increasing overall computation time.
Logical Gate: A gate operation applied to error-corrected (logical) qubits. Logical gates are built from many physical gates and are the units that high-level quantum algorithms are measured in.
Toffoli Gate: A three-qubit gate also known as the controlled-controlled-NOT (CCNOT) gate, used in many quantum algorithms, especially those related to arithmetic and factoring. It is often a bottleneck in fault-tolerant quantum circuits due to its complexity.
Gate Time: The time it takes to perform a single quantum gate operation at the physical qubit level, typically measured in nanoseconds (for superconducting qubits) or microseconds to milliseconds (for ion traps).




